数论基础

整除

对于整数 和正整数 ，如果存在整数 使得 ，则称 能被 整除，记作 。否则，称 不能被 整除，记作 。

模运算性质

在模运算的意义下， 与 （其中 是任意整数）是等价的。如在模 意义下，-2 与 6 是等价的。

  • 加减法：
  • 乘法：

同余

对于整数 和正整数 ，如果 ，则称 与 在模 意义下同余，记作 。否则，称 与 在模 意义下不相等，记作 。

质数

试除法判定质数

题干

给定 个正整数 ，判定每个数是否是质数。

输入格式

第一行包含整数 。

接下来 行，每行包含一个正整数 。

输出格式

共 行，其中第 行输出第 个正整数 是否为质数，是则输出 Yes，否则输出 No。

数据范围


输入样例：

1
2
3
2
2
6

输出样例：

1
2
Yes
No

思路分析

直接使用试除法判断是否为质数即可。对于每个数 ，只需要判断 到 之间是否存在它的因子即可。如果存在，则 不是质数；否则， 是质数。注意建议使用 而不是 来避免乘法溢出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 9;

int n;

bool is_prime(int x)
{
    if (x <= 1)
        return false;
    for (int i = 2; i <= x / i; i++)
        if (x % i == 0)
            return false;
    return true;
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n;
    while (n--)
    {
        int x;
        cin >> x;
        if (is_prime(x))
            cout << "Yes" << '\n';
        else
            cout << "No" << '\n';
    }
}

分解质因数

题干

给定 个正整数 ，将每个数分解质因数，并按照质因数从小到大的顺序输出每个质因数的底数和指数。

输入格式

第一行包含整数 。
接下来 行，每行包含一个正整数 。

输出格式

对于每个正整数 ，按照从小到大的顺序输出其分解质因数后，每个质因数的底数和指数，每个底数和指数占一行。

每个正整数的质因数全部输出完毕后，输出一个空行。

数据范围


输入样例：

1
2
3
2
6
8

输出样例：

1
2
3
4
5
2 1
3 1

2 3

思路分析

使用试除法分解质因数即可。对于每个数 ，从 开始尝试除以每个整数 ，如果 能整除 ，则将 作为一个质因数，并统计其指数，直到 不能再整除 为止，然后继续尝试下一个整数 。重复该过程直到 被完全分解。

注意：一个数 最多只会存在一个大于 的质因数（例如 ），因此在试除法过程中，如果当前的 超过了 ，且 仍然大于 ，则此时 本身就是一个质因数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
using namespace std;

int n;

void divide(int x)
{
    for (int i = 2; i <= x / i; i++)
        if (x % i == 0) // 如果把if删去，会把非因数都输出一个0
        {
            int cnt = 0;
            while (x % i == 0)
            {
                x /= i;
                cnt++;
            }
            cout << i << ' ' << cnt << '\n';
        }
    if(x > 1) cout<<x<<' '<<1<<'\n';
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n;
    while (n--)
    {
        int x;
        cin >> x;
        divide(x);
        cout<<'\n';
    }
}

筛质数

题干

给定一个正整数 ，请你求出 中质数的个数。

输入格式

共一行，包含整数 。

输出格式

共一行，包含一个整数，表示 中质数的个数。

数据范围

输入样例：

1
8

输出样例：

1
4

思路分析

筛法1：埃氏筛法，遍历 到 之间的每个数 ，如果 是质数，则将 的所有倍数标记为非质数。最后统计所有未被标记的数即为质数的个数。时间复杂度为 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;

bool st[N];    // false为质数
int primes[N]; // 存放质数
int idx;       // 记录质数个数

// 埃式筛法的做法是：每次得到一个质数时，就把1~n范围内该质数的倍数全部标记为合数
void get_primes(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i])
        {
            primes[++idx] = i;
            for (int j = 2 * i; j <= n; j += i)
                st[j] = true;
        }
    }
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    get_primes(n);
    cout << idx;
}

筛法2：线性筛法，遍历 到 之间的每个数 ，如果 是质数，则将 存入质数数组。然后对于每个质数 ，将 标记为非质数，并且当 能被 整除时，停止内层循环。时间复杂度为 。

为什么是线性？这样的筛法保证每个数只会被它的最小质因数筛掉一次。

  • 如果 ，由于 是遍历从小到大的质数，因此 的最小质因数一定小于 ，所以 的最小质因数一定是 ，此时直接将 标记为非质数，让它被 筛掉。
  • 如果 ，说明 是 的最小质因数，因此 的最小质因数也是 ，同样让它被 筛掉。由于 能被 整除，因此 ，对于后续的质数 , 此时有 ，其最小质因数一定是 ，因此不需要再让它被 筛掉了。

综上，每个数只会被它的最小质因数筛掉，因此时间复杂度为 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 9;

bool st[N];    // false为质数
int primes[N]; // 存放质数
int idx;       // 记录质数个数

// 线性筛法的目的是让每一个合数只被它的最小质因子筛掉，实现O(n)复杂度
void get_primes(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i])
            primes[++idx] = i;
        for (int j = 1; j <= idx && primes[j] <= n / i; j++)
        {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0)
                break;
        }
    }
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    get_primes(n);
    cout << idx;
}

约数

试除法求约数

题干

给定 个正整数 ，对于每个整数 ，请你按照从小到大的顺序输出它的所有约数。

输入格式

第一行包含整数 。
接下来 行，每行包含一个整数 。

输出格式

输出共 行，其中第 行输出第 个整数 的所有约数。

数据范围


输入样例：

1
2
3
2
6
8

输出样例：

1
2
1 2 3 6 
1 2 4 8

思路分析

使用试除法求约数。对于每个数 ，从 到 遍历每个整数 ，如果 能整除 ，则将 和 作为约数存储起来。为了保证输出的约数是从小到大的顺序，可以使用vector<int>存储，最后sort排序后输出。

注意：如果 和 相等（即 是 的平方根），则只需存储一次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <bits/stdc++.h>
using namespace std;

vector<int> get_divisors(int x)
{
    vector<int> divisors;
    for(int i = 1; i <= x / i; i++)
    {
        if(x % i == 0)
        {
            divisors.push_back(i);
            if(i != x / i)
                divisors.push_back(x / i);
        }
    }
    sort(divisors.begin(),divisors.end());
    return divisors;
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    while (n--)
    {
        int x;
        cin >> x;
        vector<int> res = get_divisors(x);
        for(auto ele : res)
            cout << ele << ' ';
        cout << '\n';
    }
}

约数个数

题干

给定 个正整数 ，请你输出这些数的乘积的约数个数，答案对 取模。

输入格式

第一行包含整数 。
接下来 行，每行包含一个整数 。

输出格式

输出一个整数，表示所给正整数的乘积的约数个数，答案需对 取模。

数据范围


输入样例：

1
2
3
4
3
2
6
8

输出样例：

1
12

思路分析

使用试除法分解质因数，统计每个质因数的指数。根据约数个数的公式，如果一个数 的质因数分解为 ，则 的约数个数为 ，为了便于判断质因数，可以使用unordered_map<int,int>存储质因数及其对应的指数。最后计算约数个数时需要对 取模。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int mod = 1e9 + 7;

unordered_map<int,int> factors;

void get_divisors(int x)
{
    for(int i = 2; i <= x / i; i++)
    {
        while(x % i ==0)
        {
            x /= i;
            factors[i]++;
        }
    }
    if(x > 1)
        factors[x]++;
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    while(n--)
    {
        int x;
        cin >> x;
        get_divisors(x);
    }
    ll res = 1;
    for(auto ele : factors)
        res = res * (1 + ele.second) % mod;
    cout << res;
}

约数之和

题干

给定 个正整数 ，请你输出这些数的乘积的约数之和，答案对 取模。

输入格式

第一行包含整数 。
接下来 行，每行包含一个整数 。

输出格式

输出一个整数，表示所给正整数的乘积的约数之和，答案需对 取模。

数据范围


输入样例：

1
2
3
4
3
2
6
8

输出样例：

1
252

思路分析

使用试除法分解质因数，统计每个质因数的指数。根据约数之和的公式，如果一个数 的质因数分解为 ，则 的约数之和为

即

为了便于判断质因数，可以使用unordered_map<int,int>存储质因数及其对应的指数。最后计算约数之和时需要对 取模。

注意：直接使用上述公式计算可能会导致除法问题，因此可以使用等比数列的递推关系来计算每个质因数的约数之和：

如果记，则有

因此只需对 进行 次递推即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int mod = 1e9 + 7;

unordered_map<int, int> factors;

void get_divisors(int x)
{
    for (int i = 2; i <= x / i; i++)
    {
        while (x % i == 0)
        {
            x /= i;
            factors[i]++;
        }
    }
    if (x > 1)
        factors[x]++;
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    while (n--)
    {
        int x;
        cin >> x;
        get_divisors(x);
    }
    ll res = 1; // res存放总约数之和
    for(auto ele : factors)
    {
        ll tmp = 1; // tmp存放某个质因数的约数和
        int factor = ele.first, times = ele.second;
        for(int i = 1; i <= times; i++)
            tmp = (1 + tmp * factor) % mod;
        res = res * tmp % mod;
    }
    cout << res;
}

最大公约数

题干

给定 对正整数 ，请你求出每对数的最大公约数。

输入格式

第一行包含整数 。

接下来 行，每行包含一个整数对 。

输出格式

输出共 行，每行输出一个整数对的最大公约数。

数据范围


输入样例：

1
2
3
2
3 6
4 6

输出样例：

1
2
3
2

求最大公约数可以使用辗转相除法（欧几里得算法）。对于每对数 ，不断用较大的数除以较小的数，直到余数为 ，此时较小的数即为最大公约数。

为什么辗转相除法正确？设 ，则 。因为如果一个数 能同时整除 和 ，则它也能整除 （其中 是任意整数），因此 和 有相同的约数，从而它们的最大公约数也相同。直到 时， 就是 和 的最大公约数。

补充：有公式

因此求最小公倍数也可以通过最大公约数来计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;

int gcd(int a, int b)
{
    if (!b)
        return a;
    return gcd(b, a % b);
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    while (n--)
    {
        int a, b;
        cin >> a >> b;
        cout << gcd(a, b) << '\n';
    }
}

欧拉函数

中与 互质的数的个数被称为欧拉函数，记为 。
若在算数基本定理中，，则：

亦即：

对于欧拉函数，有欧拉定理：若 与 互质，则有

当 为质数 时，，此时欧拉定理即为费马小定理：若 与 互质，则有

欧拉函数

题干

给定 个正整数 ，请你求出每个数的欧拉函数。

输入格式

第一行包含整数 。
接下来 行，每行包含一个正整数 。

输出格式

输出共 行，每行输出一个正整数 的欧拉函数。

数据范围


输入样例：

1
2
3
4
3
3
6
8

输出样例：

1
2
3
2
2
4

思路分析

使用试除法分解质因数，将质因数代入公式计算即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

ll euler(int x)
{
    ll res = x;
    for(int i = 2; i <= x / i; i++)
    {
        if(x % i == 0)
        {
            res = res * (i - 1) / i;
            while(x % i == 0)
                x /= i;
        }
    }
    if(x > 1)
    res = res * (x - 1) / x;
    return res;
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    while(n--)
    {
        int x;
        cin >> x;
        cout << euler(x) << '\n';
    }
}

筛法求欧拉函数

题干

给定一个正整数 ，求 中每个数的欧拉函数之和。

输入格式

共一行，包含一个整数 。

输出格式

共一行，包含一个整数，表示 中每个数的欧拉函数之和。

数据范围

输入样例：

1
6

输出样例：

1
12

思路分析

这类筛某种数的问题，可以根据类似线性筛法的思路来实现。观察欧拉函数的公式：

如果两个数 和 的质因数相同，则它们的欧拉函数只相差了一个系数，也就是 ；

如果两个数 和 的质因数不同，且 ，其中 是 的一个质因数而不是 的质因数，则

  • 若 是质数，则
  • 若 不是质数，按照线性筛法的思路，接下来会遍历所有 ，将 标记为非质数。
    • 若 ，则
    • 若 ，则 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;

int n;
int phi[N], primes[N], idx;
bool st[N];

void get_eulers(int n)
{
    phi[1] = 1;
    for (int i = 2; i <= n; i++)
    {
        if (!st[i])
        {
            phi[i] = i - 1;
            primes[++idx] = i;
        }
        for (int j = 1; j <= idx && primes[j] <= n / i; j++)
        {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0)
            {
                phi[i * primes[j]] = phi[i] * primes[j];
                break;
            }
            else
                phi[i * primes[j]] = phi[i] * (primes[j] - 1);
        }
    }
}

int main()
{
    cin >> n;
    get_eulers(n);
    ll res = 0;
    for (int i = 1; i <= n; i++)
        res += phi[i];
    cout << res << '\n';
    return 0;
}

快速幂

快速幂

题干

给定 组 ，对于每组数据，求出 的值。

输入格式

第一行包含整数 。
接下来 行，每行包含三个整数 。

输出格式

对于每组数据，输出一个结果，表示 的值。

每个结果占一行。

数据范围


输入样例：

1
2
3
2
3 2 5
4 3 9

输出样例：

1
2
4
1

思路分析

快速计算的结果：先预处理
、、、
即
、、、、
然后将k转化为二进制，例如，则，只要乘以k为1的位的预处理的数就行，即、，即可得到答案

预处理方法：如果已知，则

因此只需要每次对上一次的结果平方并对取模即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

ll qmi(int a, int k, int p)
{
    ll res = 1;
    while (k)
    {
        if (k & 1)
            res = res * a % p;
        k >>= 1;
        a = (ll) a * a % p;
    }
    return res;
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    while (n--)
    {
        int a, k, p;
        cin >> a >> k >> p;
        cout << qmi(a, k, p) << '\n';
    }
    return 0;
}

快速幂求逆元

题干

给定 组 ，其中 是质数，求 模 的乘法逆元，若逆元不存在则输出 impossible。

注意：请返回在 之间的逆元。

乘法逆元的定义

若整数 ， 互质，并且对于任意的整数 ，如果满足 ，则存在一个整数 ，使得 ，则称 为 的模 乘法逆元，记为 。

存在乘法逆元的充要条件是 与模数 互质。当模数 为质数时， 即为 的乘法逆元。

输入格式

第一行包含整数 。

接下来 行，每行包含一个数组 ，数据保证 是质数。

输出格式

输出共 行，每组数据输出一个结果，每个结果占一行。
若 模 的乘法逆元存在，则输出一个整数，表示逆元，否则输出 impossible。

数据范围


输入样例：

1
2
3
4
3
4 3
8 5
6 3

输出样例：

1
2
3
1
2
impossible

思路分析

为何需要逆元？

在模运算中，有加减法与乘法的分配律：

  • 加减法：
  • 乘法：
    而对于除法则没有类似的性质，也就是说

    因此就有了乘法逆元的概念：我们希望找到一个 ，使得

设

假设存在乘法逆元 满足

将 (1) (2)乘以 ，得到

根据模运算减法性质，得到

由于我们寻找的是 的乘法逆元，而 为任意数，因此想让该式恒成立，有

即

因此我们只需要找到满足 的 就是 在模 下的乘法逆元。

逆元一定存在吗？

但我们总能找到这样的 吗？例如 ，显然不存在这样的 ，因为 永远是偶数。

设

设 ，且 ,
，则有

移项，得到

由于 是整数，因此 只能为 ，也就是说 和 必须互质，才能存在乘法逆元。

如何求逆元？

由

当 是质数时，根据费马小定理，有

即

此时， 即为 在模 下的乘法逆元，使用快速幂计算 即可。

当 不是质数时，可以使用扩展欧几里得算法求解。具体见下一题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;

ll qmi(int a, int k, int p)
{
    ll res = 1;
    while (k)
    {
        if (k & 1)
            res = res * a % p;
        k >>= 1;
        a = (ll)a * a % p;
    }
    return res;
}

int gcd(int a, int b)
{
    if (a % b == 0)
        return b;
    return gcd(b, a % b);
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    while (n--)
    {
        int a, p;
        cin >> a >> p;
        if (gcd(a, p) == 1)
            cout << qmi(a, p - 2, p) << '\n';
        else
            cout << "impossible" << '\n';
    }
}

扩展欧几里得算法

扩展欧几里得算法

题干

给定 对正整数 ，对于每对数，求出一组 ，使其满足 。

输入格式

第一行包含整数 。
接下来 行，每行包含两个整数 。

输出格式

输出共 行，对于每组 ，求出一组满足条件的 ，每组结果占一行。

本题答案不唯一，输出任意满足条件的 均可。

数据范围


输入样例：

1
2
3
2
4 6
8 18

输出样例：

1
2
-1 1
-2 1

思路分析

先介绍一个定理：

裴蜀定理

设 是不全为零的整数。那么，对于任意整数 ，都有 成立；而且，存在整数 ，使得 成立。
也就是说，不定方程有整数解，当且仅当 是 的倍数。

证明：
不妨设最大公约数为 ，则 ，，其中 互质。则左边等于 ，因此左边一定是 的倍数。

对于第二部分，我们只需要举出一组 使得 成立即可，可以用扩展欧几里得算法来求解。

扩展欧几里得算法

首先，欧几里得算法的递推公式是

我们的目标是通过下一层的状态反解出当前层的状态。不妨设当前层系数为 ，下一层系数为 ，则有

化简第二个式子，由 可知

配凑成关于 的形式，得到

由于 ，对比系数可知：

由于最后一层时 ，此时有解 ，因此可以通过递归从下往上反推出每一层的 。最终我们可以得到 的一组特解。

而对于齐次不定方程 ，其通解为

由线性代数的知识”非齐次通解=非齐次特解+齐次通解”，我们可以得到原方程 的通解为

同理，如果 即 ，则方程 的通解为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <bits/stdc++.h>
using namespace std;

int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    int x1, y1, gcd = exgcd(b, a % b, x1, y1);
    x = y1;
    y = x1 - a / b * y1;
    return gcd;
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    while (n--)
    {
        int a, b, x, y;
        cin >> a >> b;
        exgcd(a, b, x, y);
        cout << x << ' ' << y << '\n';
    }
}

线性同余方程

题干

给定 组数据 ，对于每组数求出一个 ，使其满足 ，如果无解则输出 impossible。

输入格式

第一行包含整数 。
接下来 行，每行包含一组数据 。

输出格式

输出共 行，每组数据输出一个整数表示一个满足条件的 ，如果无解则输出 impossible。
每组数据结果占一行，结果可能不唯一，输出任意一个满足条件的结果均可。

输出答案必须在 int 范围之内。

数据范围


输入样例：

1
2
3
2
2 3 6
4 3 5

输出样例：

1
2
impossible
-3

思路分析

方程 等价于方程

移项，令 ，则有

也就是说，原方程有解等价于：存在整数 使得 。根据裴蜀定理，充要条件为 。

如果 ，则使用扩展欧几里得算法求出 使得

则方程 的一组特解为

其中 。

注意：当 时，原式等价于 ，此时 即为 在模 下的乘法逆元。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;

int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    int x1, y1, gcd = exgcd(b, a % b, x1, y1);
    x = y1;
    y = x1 - a / b * y1;
    return gcd;
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    while (n--)
    {
        int a, b, m, x, y;
        cin >> a >> b >> m;
        int gcd = exgcd(a, m, x, y);
        if (b % gcd)
            cout << "impossible" << '\n';
        else 
            cout << (ll)b / gcd * x % m << '\n';
    }
}

中国剩余定理

表达整数的奇怪方式

题干

给定 个整数 和 ，求一个最小的非负整数 ，满足 。

输入格式

第 行包含整数 。
第 行：第 行包含两个整数 和 ，数之间用空格隔开。

输出格式

输出最小非负整数 ，如果 不存在，则输出 −1。

数据范围




所有 的最小公倍数在 位有符号整数范围内。

输入样例：

1
2
3
2
8 7
11 9

输出样例：

1
31

思路分析

求组合数

求组合数 I

题干

给定 组询问，每组询问给定两个整数 ，，请你输出 的值。

输入格式

第一行包含整数 。

接下来 行，每行包含一组 和 。

输出格式

共 行，每行输出一个询问的解。

数据范围


输入样例：

1
2
3
4
3
3 1
5 3
2 2

输出样例：

1
2
3
3
10
1

思路分析

根据组合数的递推公式

可以使用动态规划预处理所有组合数，时间复杂度为 ，满足本题数据范围。

注意：开始时要预处理 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2010, mod = 1e9 + 7;

ll c[N][N];

int main()
{
    for (int i = 0; i < N; i++)
        for (int j = 0; j <= i; j++)
            if (!j)
                c[i][j] = 1;
            else
                c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
    int n;
    cin >> n;
    while (n--)
    {
        int a, b;
        cin >> a >> b;
        cout << c[a][b] << '\n';
    }
    return 0;
}

求组合数 II

题干

给定 组询问，每组询问给定两个整数 ，，请你输出 的值。

输入格式

第一行包含整数 。
接下来 行，每行包含一组 和 。

输出格式

共 行，每行输出一个询问的解。

数据范围


输入样例：

1
2
3
4
3
3 1
5 3
2 2

输出样例：

1
2
3
3
10
1

思路分析

本题数据范围为 ，无法使用 的动态规划预处理组合数。可以使用组合数的定义式

则有

预处理 的阶乘及其逆元，计算组合数。
由费马小定理，由于 是质数，因此

因此可以使用快速幂计算逆元。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10, mod = 1e9 + 7;

ll fact[N], infact[N];

ll qmi(int a, int k, int p)
{
    ll res = 1;
    while (k)
    {
        if (k & 1)
            res = res * a % p;
        k >>= 1;
        a = (ll)a * a % p;
    }
    return res;
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    fact[0] = 1;
    for (int i = 1; i < N; i++)
        fact[i] = fact[i - 1] * i % mod;
    for (int i = 0; i < N; i++)  
        infact[i] = qmi(fact[i], mod - 2, mod);

    while (n--)
    {
        int a, b;
        cin >> a >> b;
        cout << fact[a] * infact[b] % mod * infact[a - b] % mod << '\n';
    }
    return 0;
}

求组合数 III

题干

给定 组询问，每组询问给定三个整数 ，其中 是质数，请你输出 的值。

输入格式

第一行包含整数 。

接下来 行，每行包含一组 。

输出格式

共 行，每行输出一个询问的解。

数据范围



输入样例：

1
2
3
4
3
5 3 7
3 1 5
6 4 13

输出样例：

1
2
3
3
3
2

思路分析

由于 和 的范围高达 ，无法直接使用阶乘定义式计算组合数。可以使用卢卡斯定理来计算。

Lucas定理


即

下面给出证明（了解即可）：

首先先把 和 分解为 进制数：

接着证明一个引理：
对于正整数 ，有

由二项式定理，有

显然，对于展开式的中间项 ，当 时， 都是 的倍数，因此

因此有

同理可证明

由同余的性质 则 可知

我们把 代入 ，得到
$$
(1 + x)^a = (1 + x)^{a_k p^k + a_{k-1} p^{k-1} + \dots + a_1 p + a_0} \

= (1 + x)^{a_k p^k} \times (1 + x)^{a_{k-1} p^{k-1}} \times \dots \times (1 + x)^{a_1 p} \times (1 + x)^{a_0}
由可知
(1 + x)^a \equiv (1+x^{p^k})^{a_k} \times (1 + x^{p^{k-1}})^{a_{k-1}} \times \dots \times (1 + x^p)^{a_1} \times (1 + x^{a_0}) \pmod {p}
$$
两边对于 比较系数，显然左式系数为 ；

由 ，可以得到

显然， 在 中的系数为 ，同理可知 在 中的系数为 ，依此类推，因此右式中 的系数为

因此有

而 ，，则

回顾 和 的 进制表示：
$$
a=(a_k a_{k-1} \dots a_1 a_0)p \
b=(b_k b{k-1} \dots b_1 b_0)p
则
a_k a{k-1} \dots a_1 = \lfloor \frac{a}{p} \rfloor \
b_k b_{k-1} \dots b_1 = \lfloor \frac{b}{p} \rfloor
因此
C_{\lfloor{\frac{a}{p}} \rfloor}^{\lfloor{\frac{b}{p}} \rfloor} \equiv C_{a_k}^{b_k} \times C_{a_{k-1}}^{b_{k-1}} \times \dots \times C_{a_1}^{b_1} \pmod p
整理得到
C_a^b \equiv C_{\lfloor{\frac{a}{p}} \rfloor}^{\lfloor{\frac{b}{p}} \rfloor} \times C_{a \bmod p}^{b \bmod p} \pmod p
$$

Lucas定理如何应用？

我们可以写一个lucas(ll a, ll b)函数，当 时直接返回 的值，否则递归调用 lucas(a/p, b/p) * C_{a mod p}^{b mod p} mod p。

1
2
3
4
5
6
ll lucas(ll a, ll b)
{
    if (a < p && b < p)
        return c[a][b];
    return (ll)lucas(a / p, b / p) * C[a % p][b % p] % p;
}

由于我们还要求 ，我们可以写一个 C(int a, int b) 函数，使用阶乘定义式计算组合数。

由于 是质数，因此可以使用快速幂计算逆元。

因为 ，即

循环总共进行 次，分子乘了 ，分母乘了 的逆元，得到最终结果。

1
2
3
4
5
6
7
8
9
10
int C(int a, int b)
{
    int res = 1;
    for (int i = 1, j = a; i <= b; i++, j--)
    {
        res = (ll)res * j % p;
        res = (ll)res * qmi(i, p - 2, p) % p;
    }
    return res;
}

再加上快速幂代码，得到最后的AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5010;

int qmi(int a, int k, int p)
{
    ll res = 1;
    while (k)
    {
        if (k & 1)
            res = res * a % p;
        k >>= 1;
        a = (ll)a * a % p;
    }
    return res;
}

int C(int a, int b, int p)
{
    ll res = 1;
    for (int i = 1, j = a; i <= b; i++, j--)
    {
        res = res * j % p;
        res = res * qmi(i, p - 2, p) % p;
    }
    return res;
}

int lucas(ll a, ll b, int p)
{
    if (a < p && b < p)
        return C(a, b, p);
    return (ll)lucas(a / p, b / p, p) * C(a % p, b % p, p) % p;
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    while (n--)
    {
        ll a, b;
        int p;
        cin >> a >> b >> p;
        cout << lucas(a, b, p) << '\n';
    }
}

求组合数 IV

题干

输入 ，求 的值。

注意结果可能很大，需要使用高精度计算。

输入格式

共一行，包含两个整数 和 。

输出格式

共一行，输出 的值。

数据范围

输入样例：

1
5 3

输出样例：

1
10

思路分析

如果按照组合数的公式来，我们不仅要写高精度乘法，还要写高精度除法，这样结果会过于复杂。我们可以考虑分解质因数法，即将组合数的分子和分母的质因数分解，统计每个质因数的指数，将分子和分母的质因数指数相减，得到最终结果的质因数指数。这样就可以避免除法运算。

接下来我们需要一个函数返回一个数的质因数分解结果。虽然试除法这题理论上也能过，但我们有更快的方法。

对于 和一个质数 ，如果我们想知道 中 的指数，可以使用以下公式：

首先， 代表 中有多少个数是 的倍数； 代表 中有多少个数是 的倍数；以此类推，直到 。显然，如果一个数为 的倍数而不是 的倍数，那么它会在算 时候被计算一次，在算 时被计算一次，总共会被计算 次，因此一定不重不漏。

我们有了计算 中 的指数的方法，那么我们就要找到 以内所有的质数（线性筛法），对 分别遍历每一个质数的指数，最后将分子和分母的质因数指数相减，得到最终结果的质因数指数，然后将结果转换为高精度数输出即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5010;

bool st[N];
int primes[N], idx;
int sum[N];

void get_primes(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i])
            primes[++idx] = i;
        for (int j = 1; primes[j] <= n / i && j <= idx; j++)
        {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0)
                break;
        }
    }
}

int fact(int n, int p)
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}

vector<int> mul(vector<int> A, int b)
{
    int t = 0;
    vector<int> ans;
    for (int i = 0; i < A.size(); i++)
    {
        t += A[i] * b;
        ans.push_back(t % 10);
        t /= 10;
    }
    while (t)
    {
        ans.push_back(t % 10);
        t /= 10;
    }
    return ans;
}

int main()
{
    int a, b;
    cin >> a >> b;
    get_primes(a);
    
    for (int i = 1; i <= idx; i++)
        sum[primes[i]] = fact(a, primes[i]) - fact(b, primes[i]) - fact(a - b, primes[i]);
    
    vector<int> res;
    res.push_back(1);
    for (int i = 1; i <= idx; i++)
        for (int j = 1; j <= sum[primes[i]]; j++)
            res = mul(res, primes[i]);
    
    for (int i = res.size() - 1; i >= 0; i--)
        cout << res[i];
    
    return 0;
}

Catalan数

满足条件的01序列

题干

给定 个 和 个 ，它们将按照某种顺序排成长度为 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 的个数都不少于 的个数的序列有多少个。

输出的答案对 取模。

输入格式

共一行，包含整数 。

输出格式

共一行，包含一个整数，表示答案。

数据范围

输入样例：

1
3

输出样例：

1
5

思路分析

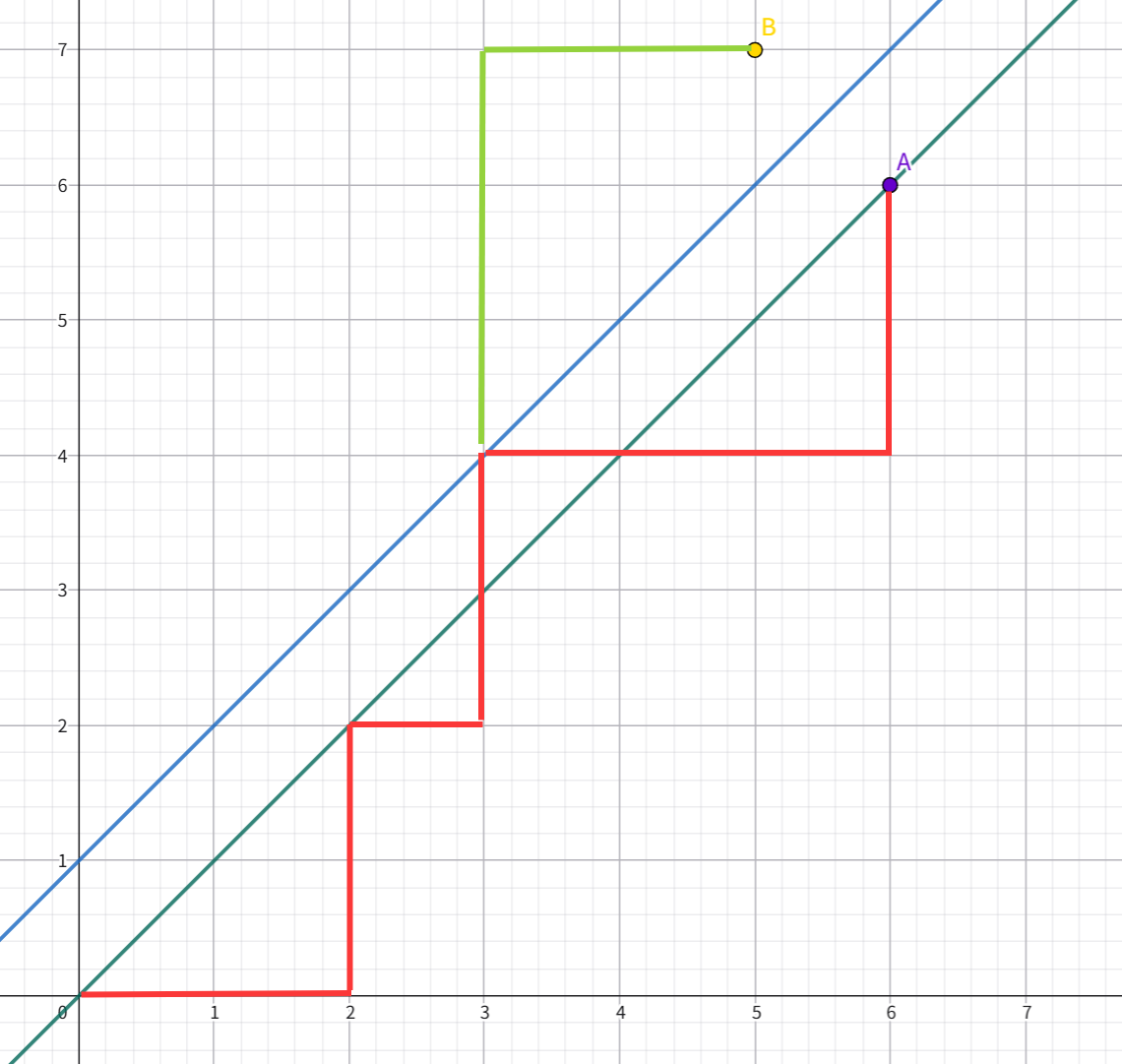
image-20251207211049973

不妨将 视为向右走一步， 视为向上走一步，那么题目就转化为从 走到 且不能走到 上方（但可以触碰）的情况下的路径总数。

此时作直线 ，则所有不符合条件的路径都必须经过这条直线（含触碰）。以 为例，所有不符合条件的路径，必然有一个第一次触碰 的点 ，将 之后的路线关于 对称映射，得到一条从 走到 ， 的路径。不难得到，不符合条件的路径数等于从 走到 的路径数。因此得到符合条件的路径数为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;

ll qmi(int a, int k, int p)
{
    ll res = 1;
    while (k)
    {
        if (k & 1)
            res = res * a % p;
        k >>= 1;
        a = (ll)a * a % p;
    }
    return res;
}

int main()
{
    int n;
    cin >> n;
    ll res = 1;
    for (int i = 1, j = 2 * n; i <= n; i++, j--)
    {
        res = res * j % mod;
        res = res * qmi(i, mod - 2, mod) % mod;
    }
    res = res * qmi(n + 1, mod - 2, mod) % mod;
    // 注意最后的 /(n + 1) 记得用逆元
    cout << res;
}

容斥原理

能被整除的数

题干

给定一个整数 和 个不同的质数 。

请你求出 中能被 中的至少一个数整除的整数有多少个。

输入格式

第一行包含整数 和 。

第二行包含 个质数。

输出格式

输出一个整数，表示满足条件的整数的个数。

数据范围

输入样例：

1
2
10 2
2 3

输出样例：

1
7

思路分析

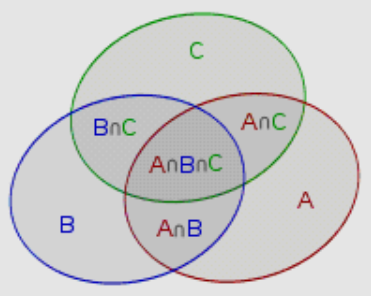
image

由Venn图可知，三个集合的容斥原理为

推广到一般情况下，设有 个集合 ，则容斥原理为

对于本题，设 表示能被 整除的数的集合，不难证明 。

由于 都是质数，因此 ，也就是说 。

我们只需要枚举所有的子集，计算每个子集的大小，根据容斥原理，如果子集是奇数个质数的乘积，则加上该子集的大小，否则减去该子集的大小。

显然共有 个非空子集，并且每一个 要么出现，要么不出现，因此可以使用二进制状态压缩枚举每一个子集。将 个质数分别对应二进制的 位，枚举 的每一个状态，对于每一个状态枚举每一位，如果该位为 ，则将对应的质数乘到当前子集的乘积中，并且记录当前子集质数的个数；如果最后质数个数为奇数，就加上 乘积，否则减去。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 20;

int p[N];

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; i++)
        cin >> p[i];
    
    int res = 0;
    // res记录最后的总数
    for (int i = 1; i < 1 << m; i++) // 枚举所有非空子集
    {
        int t = 1, cnt = 0;
        // t记录当前子集质数的乘积，cnt记录当前子集质数的个数
        for (int j = 0; j < m; j++)
        {
            if (i >> j & 1)
            {
                cnt++;
                if ((ll)t * p[j] > n)
                {
                    t = -1;
                    break;
                }
                // 如果质数乘积超过n，显然该子集对结果没有贡献，直接跳出
                t *= p[j];
            }
        }
        
        if (t != -1)
        {
            if (cnt & 1) res += n / t;
            // 如果质数个数为奇数，加上该子集大小
            else res -= n / t;
            // 否则减去该子集大小
        }
    }
    cout << res << '\n';
    return 0;
}

博弈论

891.Nim游戏

题干

给定 堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式

第一行包含整数 。

第二行包含 个数字，其中第 个数字表示第 堆石子的数量。

输出格式

如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围


每堆石子数

输入样例：

1
2
2
2 3

输出样例：

1
Yes

思路分析

先以 堆石子为例：

设两堆石子的数量分别为 和 。
如果先手先从第二堆拿走 个石子，则变为 ，无论后手从哪一堆拿走多少个石子，先手都可以对另一堆做出相同的操作，保证两堆石子的数量始终相等，最终先手必胜。

设如果两堆石子的数量分别为 和 。
此时先手无论从哪一堆拿走多少个石子，后手都可以对另一堆做出相同的操作，保证两堆石子的数量始终相等，最终后手必胜。

我们可以将所有状态分为两类：先手必胜状态和先手必败状态。
例如， 是先手必胜状态，而 是先手必败状态。

  • 对于先手必胜状态，存在一种操作，使得这次操作后变为先手必败状态。此时对面必败，则我方必胜。
  • 对于先手必败状态，无论做出什么操作，都会变为先手必胜状态。此时对面必胜，则我方必败。

我们想：是否存在一种运算，使得其运算性质与Nim游戏的输赢状态完全一致？异或运算就是我们要找的答案。

Nim和

自然数 的Nim和定义为

Nim和与Nim游戏的关系

Nim游戏中，状态是必败状态，当且仅当Nim和

证明

  1. 若 对于所有 都成立，此时为先手必败状态，并且Nim和为0，原命题成立。
  2. 若

    要证明此状态是先手必胜状态，只需证明存在一个合法操作使得该操作后变为先手必败状态。不妨设 的二进制表示中，最高位为 的位数是第 位，则必然存在 使得 第 位为 。接下来必然有 ，因为和 相比，的第 位变为 ，而最高位不变。那么我们做一个操作：将 变为 ，由于 则该操作必然合法。此时我们有

    即必然存在一个合法操作，使得操作完变为先手必败状态。
  3. 若

    则对于任何合法操作，操作后Nim和都会变为非0。使用反证法：假设存在 ，使得其通过合法操作变为 后Nim和仍为 ，则有

    则有

    由

    可知

    因此

    由于必须要拿至少一个石块，因此这不是一个合法操作。也就是说对于任何合法操作，操作后Nim和都会变为非0。

因此异或运算Nim和的规则与Nim游戏完全相同，因此我们可以用异或运算计算一个Nim游戏是否为先手必胜。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <bits/stdc++.h>
using namespace std;

int main()
{
    int n;
    cin >> n;
    int res = 0;
    while (n--)
    {
        int x;
        cin >> x;
        res ^= x;
    }
    if (res) 
        cout << "Yes" << '\n';
    else 
        cout << "No" << '\n';
}

892.台阶-Nim游戏

现在，有一个 级台阶的楼梯，每级台阶上都有若干个石子，其中第 级台阶上有 个石子()。

两位玩家轮流操作，每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中（不能不拿）。

已经拿到地面上的石子不能再拿，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式

第一行包含整数 。

第二行包含 个整数，其中第 个整数表示第 级台阶上的石子数 。

输出格式

如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围


输入样例：

1
2
3
2 1 3

输出样例：

1
Yes

思路分析

我们先枚举几个台阶数较小的情况，找找规律：

当 时，只有一堆石子，先手必胜当且仅当 。

当 时，有两堆石子。

  • 如果 ，那么无论先手将多少个石子从二级拿到一级，后手只需要将这些石子再从一级拿到地面即可，因此先手必败。
  • 如果 ，先手可以将一级的石子全部拿到地面，此时给对面构造出 先手必败的情况，所以此时先手必胜。

也就是说当 时，先手必胜当且仅当 。好像与第二级台阶无关？

我们考虑一个情况：如果只有偶数台阶上有石子，而奇数台阶上没有石子，那么无论先手如何操作，后手都可以将先手从偶数台阶拿到奇数台阶的石子再拿回偶数台阶，从而保证奇数台阶始终没有石子，因此后手必胜，先手必败。

提出一个假设：偶数台阶的石子情况可能不影响整个有向图游戏的结果。

也就是说，整个有向图游戏的结果只与 有关；当奇数台阶石子全为 时，也就是只有偶数台阶有石子时，先手必败。此时

当奇数台阶有石子并且 时，无论先手如何操作，操作后留给后手的状态必然有

当奇数台阶有石子并且 时，此时移动石子不会影响其他奇数台阶的状态，由经典Nim游戏可知先手必然存在一种操作使得

也就是说，若奇数台阶异或和不为 ，则先手每次都可以留给对方奇数台阶异或和为 的状态，从而让下一轮对方留给自己奇数台阶异或和不为 的状态；当奇数台阶石子全部为 时，此时一定是对方遇到这种这种情况，也就是说对方遇到了先手必败情况，因此先手必胜。奇数台阶异或和为 则反之。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <bits/stdc++.h>
using namespace std;

int main()
{
    int n;
    cin >> n;
    int res = 0;
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        if (i & 1)
            res ^= x;
    }
    if (res)
        cout << "Yes" << '\n';
    else 
        cout << "No" << '\n';
    return 0;
}

893.集合-Nim游戏

题干

给定 堆石子以及一个由 个不同正整数构成的数字集合 。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 ，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式

第一行包含整数 ，表示数字集合 中数字的个数。

第二行包含 个整数，其中第 个整数表示数字集合 中的第 个数 。

第三行包含整数 。

第四行包含 个整数，其中第 个整数表示第 堆石子的数量 。

输出格式

如果先手方必胜，则输出 Yes。
否则，输出 No。

数据范围


输入样例：

1
2
3
4
2
2 5
3
2 4 7

输出样例：

1
Yes

思路分析

先介绍一个函数：函数。

即为不在A集合中的最小自然数。

Sprague-Grundy定理

对于一个无向图表示的无环博弈，每个状态对应一个非负整数，称为该状态的SG值。SG值的定义如下：

  • 终止状态的SG值为 。
  • 其他状态的SG值为所有后继状态的SG值的Mex值。
  • 对于多个子博弈的合成博弈，其SG值为各个子博弈SG值的异或和。
  • 一个状态是先手必败状态，当且仅当该状态的SG值为 。
  • 一个状态是先手必胜状态，当且仅当该状态的SG值不为 。
  • 对于Nim游戏，每堆石子的数量即为该堆石子的SG值，整个游戏的SG值为各堆石子数量的异或和。
  • 对于本题，设 表示石子数量为 的堆的SG值，则有

    以本题样例为例。对于石子数量为 的堆，显然 ；

对于石子数量为 的堆，无法拿到 或 个石子，因此 ；

对于石子数量为 的堆，可以拿到 个石子，变为 个石子，因此 ；

对于石子数量为 的堆，可以拿到 个石子，变为 个石子，因此 ；

对于石子数量为 的堆，可以拿到 个石子，变为 个石子，因此 ；

对于石子数量为 的堆，可以拿到 个石子，变为 个石子，或者拿到 个石子，变为 个石子，因此 ；

以此类推，可以计算出 分别为 。由于题目中有 堆石子，数量分别为 ，因此整个游戏的SG值为 ，因此先手必胜，输出 Yes。

为什么这个定理正确？

先从单个博弈开始分析：

  1. 终止状态的SG值为 ，显然正确，因为无法进行操作的人视为失败。
  2. 其他状态的SG值为所有后继状态的SG值的Mex值。
    • 如果一个状态的SG值为 ，则该状态的所有后继状态的SG值都不为 ，否则该状态的SG值就不为 了。因此对于先手必败状态，无论做出什么操作，都会变为先手必胜状态。
    • 如果一个状态的SG值不为 ，则该状态至少存在一个后继状态的SG值为 ，否则该状态的SG值就为 了。因此对于先手必胜状态，存在一种操作，使得这次操作后变为先手必败状态。
  3. 也就是说，SG值的定义与先手必胜状态和先手必败状态的定义完全一致，因此该定义是正确的。

接下来分析多个子博弈的合成博弈：

  1. 如果合成博弈的SG值为 ，则对于任何一种操作，都会使得合成博弈的SG值不为 。
    • 设有 个子博弈，子博弈的SG值分别为 ，则合成博弈的SG值为 。
    • 设进行一次操作后，第 个子博弈的SG值变为 ，则合成博弈的SG值变为 。
    • 由于 ，因此
    • 由于进行一次操作后，第 个子博弈的SG值必然发生变化，因此 ，则 。因此合成博弈的SG值不为 。
  2. 如果合成博弈的SG值不为 ，则存在一种操作，使得合成博弈的SG值变为 。
    • 设有 个子博弈，子博弈的SG值分别为 ，则合成博弈的SG值为 。
    • 类比Nim游戏的证法，必然存在 。那么我们做一个操作：将第 个子博弈的SG值变为 。由于第 个子博弈的SG值为 ，说明其后继状态包含了 中的所有数，又因为 ，则 可以取到。因此该操作是合法的。此时合成博弈的SG值变为
    • 因此必然存在一种操作，使得合成博弈的SG值变为 。

因此多个子博弈的合成博弈的SG值与先手必胜状态和先手必败状态的定义完全一致，因此该定义是正确的。

对于代码实现，求 的过程类似于动态规划中的记忆化搜索，按照动态规划做法完成即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 110, M = 10010;

int S[N], f[M];
int k, n;
// f[i]表示sg(i)

int sg(int x)
{
    if (f[x] != -1)
        return f[x];
    // 记忆化搜索避免重复计算
    unordered_set<int> next;
    // 将后继状态存到set中，set查找的复杂度是O(log n)，更快捷方便求mex
    for (int i = 1; i <= k; i++)
        if (x >= S[i])
            next.insert(sg(x - S[i]));
    for (int i = 0;; i++)
        if (!next.count(i))
        {
            f[x] = i;
            return f[x];
        }
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    memset(f, -1, sizeof f);
    cin >> k;
    for (int i = 1; i <= k; i++)
        cin >> S[i];
    cin >> n;
    int res = 0;
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    if (res)
        cout << "Yes";
    else
        cout << "No";
}

894.拆分-Nim游戏

题干

给定 堆石子，两位玩家轮流操作，每次操作可以取走其中的一堆石子，然后放入两堆规模更小的石子（新堆规模可以为 ，且两个新堆的石子总数可以大于取走的那堆石子数），最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式

第一行包含整数 。

第二行包含 个整数，其中第 个整数表示第 堆石子的数量 。

输出格式

如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围

输入样例：

1
2
2
2 3

输出样例：

1
Yes

思路分析

对于一堆规模为 的石子，可以分为两堆规模分别为 和 的石子， 其中 。由于操作过后石子规模的最大值会变小，因此经过足够次操作后游戏一定会结束，也就是说这是个无环博弈，可以使用Sprague-Grundy定理。

设 表示石子数量为 的堆的SG值，考虑其后继状态，以 为例，可以分为 六种情况。对于情况 ，我们又可以将其分为两个子博弈，子博弈的SG值分别为 和 ，因此该情况的SG值为 。综上所述，我们有

得到公式后使用记忆化搜索计算每个 ，最后将所有堆的SG值异或即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 110, M = 10010;

int S[N], f[M];
int k, n;
// f[i]表示sg(i)

int sg(int x)
{
    if (f[x] != -1)
        return f[x];
    unordered_set<int> next;
    for (int i = 0; i < x; i++)
        for (int j = 0; j < x; j++)
            next.insert(sg(i)^sg(j));

    for (int i = 0; ; i++)
        if (!next.count(i))
        {
            f[x] = i;
            return f[x];
        }
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    memset(f, -1, sizeof f);

    cin >> n;
    int res = 0;
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    if (res)
        cout << "Yes";
    else
        cout << "No";
}